Showball Problem Journal
Problem
Matt is a mathematician and so in a how-big-can-your-snowball-get competition for some reason people trusted him to weigh the snowballs. He annoyingly weighs the snowballs two at a time (not sure how he held and fit the snowballs), producing 2210, 2270, 2310, 2330, 2370, 2400, 2430, 2460, 2520, and 2560 in an unknown unit of weight. Now, the students of JLS are inconveniently tasked with finding the weights of the snowballs.
Update 1
Trying to make a brute-force program that checks all the possibilities through trial and error.
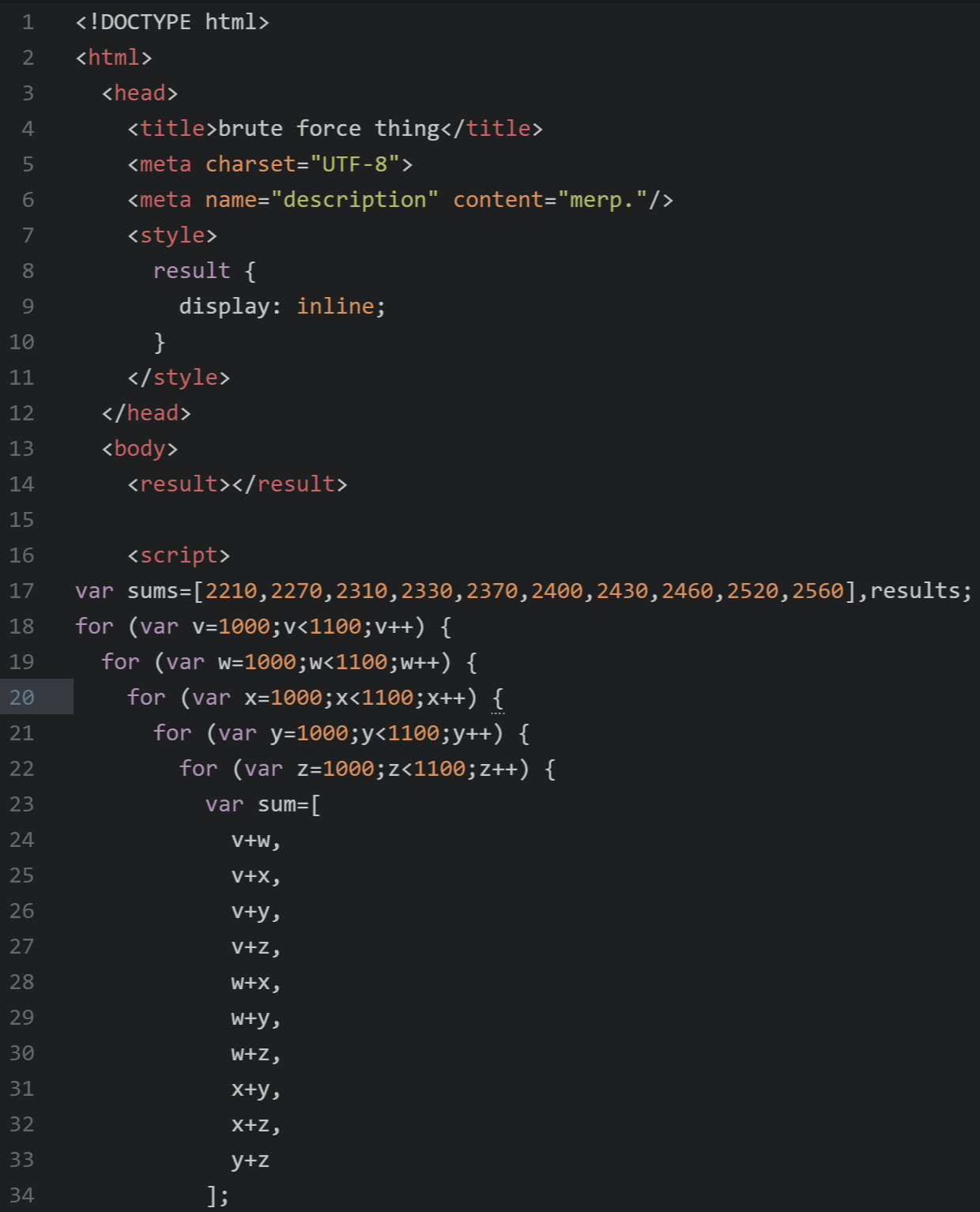
A bit into the program and I decided that for the sake of my education and computer, I’d be better off actually trying to solve it with legit math.
Update 2
I know eval is evil, but the sum of all the weights is

Assuming variables v-z are the snowball weights,
4v+4w+4x+4y+4z=23860
Not sure if that’ll be useful, but ah well.
Of course, I could just always ask Google how to do these types of problems.
Update 3
Obviously, that means that the sum of all the snowballs’ weights is
v+w+x+y+z=5965
The mean of the weights is 1193.
Also, assuming the variables v-z are in order from smallest snowball to biggest,
v+w=2210 and y+z=2560
Update 4
Stumped, I Googled “weight two at a time solution” and saw something like
... = 5 * (an average)
Thinking I got something and, being a greedy human I am and wanting to solve this by myself, I quickly closed the tab.
Then I realized I could just do
2210+x+2560=5965
x+4770=5965
x=1195
Yay I have just found the 3rd place snowball!
I’m quite certain that v+x=2270 and x+z=2520, so I’m going to solve for v and z, then w and y, and then use JavaScript to check.
Update 5
All my answers were whole numbers, so they’re likely correct.
showball results
placement|weight in unit —:|— 1st|1325 2nd|1235 3rd|1195 4th|1135 last|1075
Time to weigh them!
Update 6
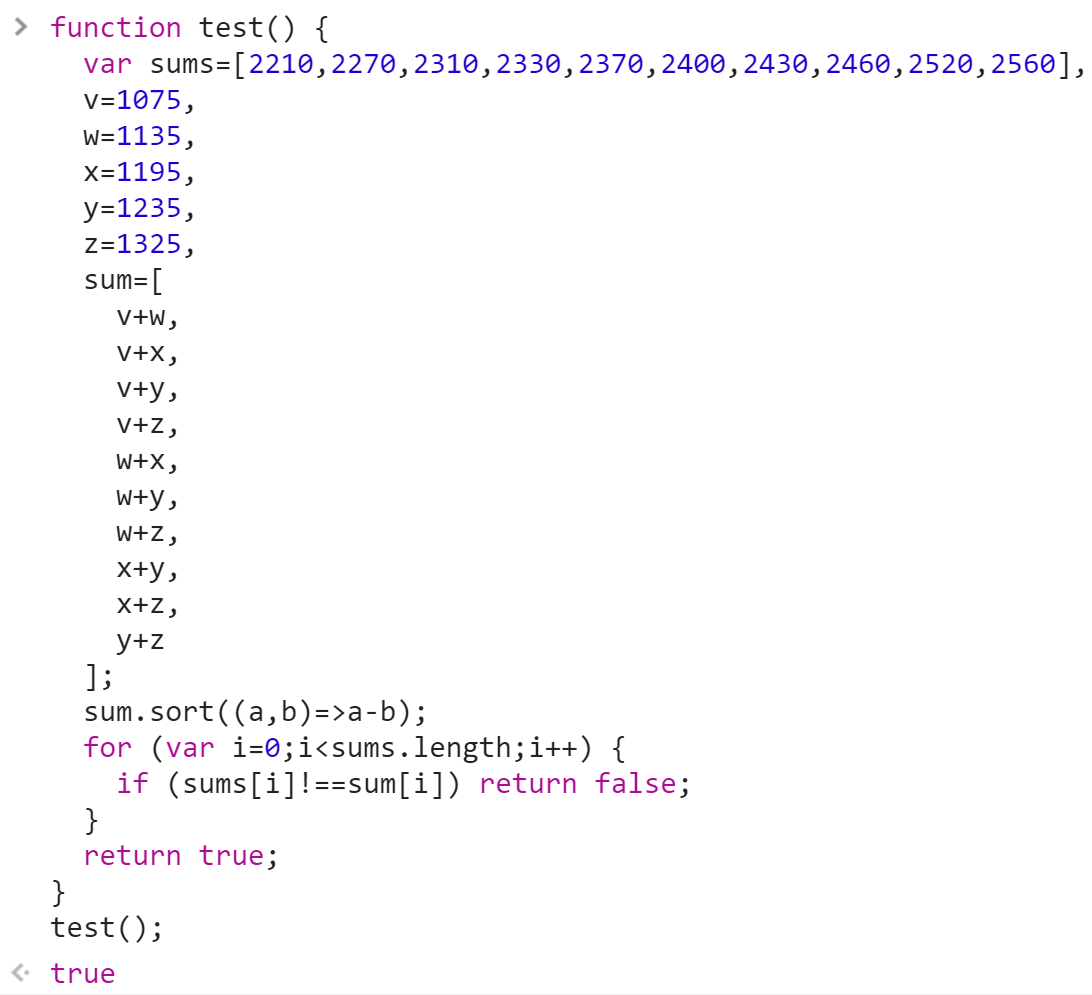
JavaScript has created the snowballs of my weights, weighed them two at a time, then compared them with Matt’s combinations. They match!
Lesson learned: don’t weigh things two at a time.